Cum să găsiți zona unui trapez?

Înainte de a găsi zona trapezului, este necesar să se dea definiția sa.

Trapezul este o figură geometrică cu patruunghiuri, în care cele două laturi sunt paralele unul cu altul, iar celelalte două nu sunt. Două laturi, care sunt paralele una cu cealaltă, sunt numite baze, iar cele laterale paralele. Dacă laturile laterale sunt egale, trapezoidul va fi numit isoscele. Dacă formează un unghi drept la intersecție, este dreptunghiular.

În algebră, există și conceptul de trapezoid curbilinar, prin aceasta se înțelege o figura delimitată pe o parte de axa x, iar pe de altă parte printr-un grafic al funcției y = f (x) b și definit pe intervalul [a; b]

Cum să găsiți zona unui trapez

O astfel de figură geometrică este calculată prin formula S = 0,5 * (a + b) * h, unde a și b sunt lungimile bazelor trapezoidale și h este înălțimea ei.

Un exemplu. Având un trapez, o bază de 2 cm, a doua - 3 cm și o înălțime de 4 cm. Se calculează suprafața cu formula, obținem rezultatul: S = 0, 5 * (2 + 3) * 4 = 12 cm2.

Din aceeași formulă rezultă că, știind aria acestei figuri, înălțimea ei, lungimea uneia dintre laturi, se poate găsi lungimea celeilalte. A doua opțiune - cunoașterea lungimii laturilor și a zonei trapezoidului, îi puteți găsi înălțimea.

Un exemplu. Se dă un trapez, în care o bază este de 3 ori mai lungă decât cealaltă. Înălțimea figurii este de 3 cm, suprafața este de 24 cm2. Este necesar să se găsească lungimea ambelor baze.

Soluția. Zona se calculează după următoarea formulă: S = 0,5 * (a + b) * h. Din condițiile problemei este clar că o parte este de trei ori mai mare decât cealaltă, deci a = 3c. Înlocuim a în formula și obținem S = 0.5 * (3c + c) * h = 0.5 * 4c * h. Ca rezultat, obținem S = 2v * h, adică, = S / 2h. Înlocuiți valorile numerice și obțineți 6 = 6 cm, a = 18 cm.

Cu toate acestea, acest lucru nu este singurul mod în careputeți stabili aria acestei cifre. Conform celei de-a doua metode, înainte de a găsi zona trapezului, îl puteți împărți în figuri geometrice simple: un dreptunghi și două triunghiuri (sau un triunghi, dacă este un trapez dreptunghiular). În acest caz, suprafața totală va fi calculată ca sumă a zonelor acestor cifre. Ca opțiune, o puteți introduce într-un dreptunghi, a cărui latură va fi egală cu lungimea celei mai mari baze. În acest caz, suprafața trapezoidului este definită ca diferența dintre zonele dreptunghiului și triunghiurile.

Cum să găsiți zona unui trapez dreptunghiular? Anterior sa spus că un trapez dreptunghiular poate fi numit un trapez, în care baza (să zicem a) și partea cu intersecția, formând un colț. În consecință, în această figură, partea avsd a lui c va fi înălțimea. Apoi, cunoscând lungimea tuturor celor trei laturi, se poate găsi aria figurului S = 0.5 * (a + b) * s.

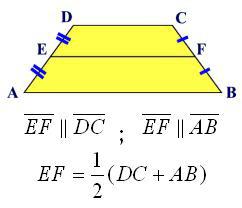
Formula cea mai simplă arată astfel: S = k * h, unde k este lungimea liniei mediane a trapezoidului, h este înălțimea acestuia. Problema este că, în practică, este mai ușor să se măsoare lungimea bazelor decât să se găsească linia de mijloc. Și este după cum urmează:

având în vedere: scalen, non-dreptunghiulare trapez AVSD unde laturile AB și CD sunt bazele. Înainte de a găsi zona trapezului ar trebui să segmente de curent alternativ și VD împărțit în 2 părți egale, marcând punctul de intersecție dintre literele G și C. Apoi, CC linie, a avut loc paralel cu solul, și va fi linia mediană a trapez m.

Un alt caz special este atunci când trapezulechilateral. Pentru aceasta, toate formulele de mai sus (bineînțeles, cu excepția formulelor pentru dreptunghiulare) vor face. Suprafața sa poate fi determinată prin cunoașterea unghiului dintre baze. Formula este după cum urmează: S = (a + b) * c * sin (x) * 0.5, unde a și b sunt lungimile bazelor, c este lungimea laturii și x este unghiul dintre ele.

Uneori devine necesară determinarea zoneiAceastă cifră nu este numai în geometrie, ci și în algebră în sistemul de coordonate. În acest sens, elevii au întrebarea cum să găsească zona de trapez prin coordonate. Principiul de calcul este același - determinați lungimile laturilor, ca diferență în coordonatele punctelor de bază, calculați înălțimea și calculați suprafața cu prima formulă. Înălțimea va fi o linie dreaptă trasă din colțul unei baze în cealaltă bază.

Integralul este folosit pentru a determina zona trapezoidului curbilinar.